Coin Change

322. Coin Change

source: https://leetcode.com/problems/coin-change/

Question

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

暴力法

这个问题，可以被拆分为重叠的子问题时。有点类似70题。

/**
 * 暴力法
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = function (coins, amount) {
    if (amount === 0) return 0;
    if (amount < 0) return -1;
    let ret = Infinity;
    for (let coin of coins) {
        // 如果是此硬币补上最后一个硬币的最优解
        const sub = coinChange(coins, amount - coin);
        // 此硬币补不上
        if (sub < 0) continue;
        // 此硬币可以补上，同时比较和其他硬币的最优解
        ret = Math.min(ret, sub + 1);
    }
    return ret === Infinity ? -1 : ret;
};

这种解法比较简单容易想到，缺点是有很多重复计算，可以看一下其形成的迭代树:

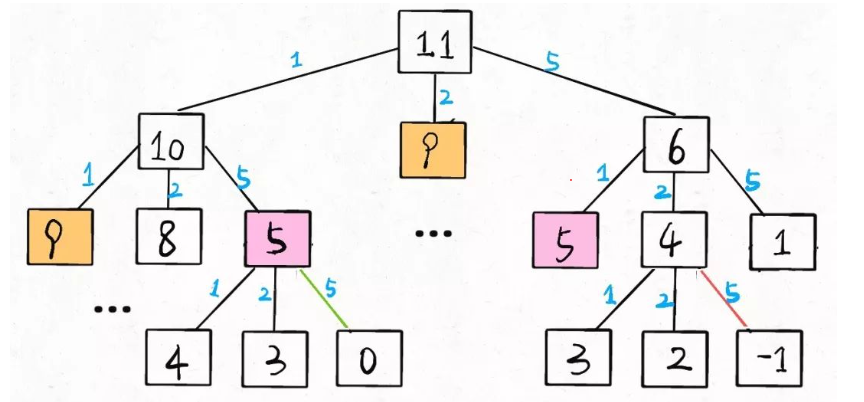
增加备忘录

看了迭代树，其实很容易想到增加备忘录，类似斐波那契数列的优化：

/**
 * 暴力法+备忘录
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = function (coins, amount) {
    const cache = {};
    const run = (n) => {
        if (n === 0) return 0;
        if (n < 0) return -1;
        let ret = Infinity;
        for (let coin of coins) {
            const key = n - coin;
            if (!cache[key]) cache[key] = run(key);
            if (cache[key] < 0) continue;
            ret = Math.min(ret, cache[key] + 1);
        }
        return ret === Infinity ? -1 : ret;
    }
    return run(amount);
};

dp

先明确一下dp时的定义：

• 明确状态：由于硬币是无线的，转移的状态是目标金额amount
• 确定dp数组定义：dp[n]代表当前金额为n的最优解
• 明确选择：从coins中选择一个硬币，然后减少目标金额
• 明确base case：目标金额为0时，返回0; 目标金额小于0时，按题意返回-1

/**
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = function (coins, amount) {
    const dp = new Array(amount + 1).fill(amount + 1);
    dp[0] = 0;
    for (let i = 1; i < dp.length; i++) {
        for (let coin of coins) {
            const left = i - coin;
            if (left < 0) continue;
            dp[i] = Math.min(dp[i], dp[left] + 1);
        }
    }
    return dp[amount] === amount + 1 ? -1 : dp[amount];
};

总结

这道题的核心，或者说所有dp题目的核心，还是要推出状态转变公式，这样的话无论是加缓存还是用dp，都是可以的。