Last Commit: 2024-01-06 17:50:27
views:
Sorting Algorithm
Bubble Sort
Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.
((arr)=>{
for (let i = arr.length -1; i > 0; i--){
for (let j = 0; j < i; j++){
if (arr[j] > arr[j+1]){
let temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
})(Array(100).fill(null).map(() => Math.round(Math.random()*100)));
Selection Sort
It is the reverse of Bubble Sorting.
((arr)=>{
for (let i=0;i<arr.length;i++){
for (let j=i+1;j<arr.length;j++){
if (arr[j] < arr[i]){
let temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
}
}
return arr;
})(Array(100).fill(null).map(() => Math.round(Math.random()*100)));
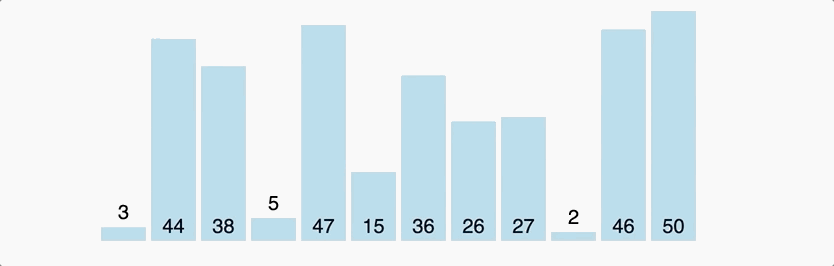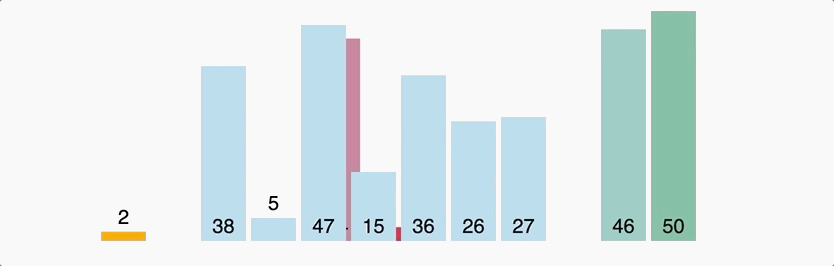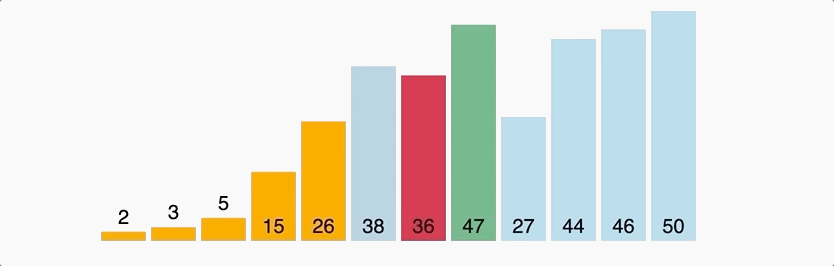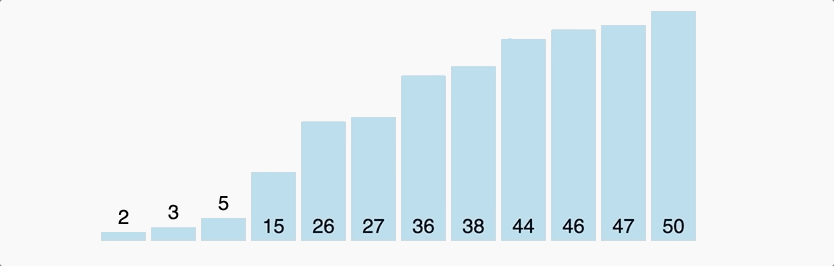
Quick Sort
A typical implementation of Divide-and-Conquer Method, selecting a pivot and using it to split the array to two part.
Normally, its time complexity is n(nlogn). In worst situation that the first selected pivot is the extremum of the array, its time complexity is n(n^2).
(_arr=>{
const quickSort = arr => {
if (arr.length < 2) return arr;
const pivot = arr.pop();
return [...quickSort(arr.filter(item => item < pivot)), pivot, ...quickSort(arr.filter(item => item >= pivot))];
};
return quickSort(_arr);
})(Array(100).fill(null).map(() => Math.round(Math.random()*100)));
Insert Sort
Shell Sort
Heap Sort
Heap sort is a comparison-based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the minimum element and place the minimum element at the beginning. We repeat the same process for the remaining elements.
The process of reshaping a binary tree into a Heap data structure is known as 'heapify'. A binary tree is a tree data structure that has two child nodes at max. If a node’s children nodes are 'heapified', then only ‘heapify’ process can be applied over that node. A heap should always be a complete binary tree.
Starting from a complete binary tree, we can modify it to become a Max-Heap by running a function called ‘heapify’ on all the non-leaf elements of the heap. i.e. ‘heapify’ uses recursion.
(_arr => {
/**
* heap sort
* @param {number[]} arr
* @returns
*/
const heapSort = arr => {
/**
* swap value in arr
* @param i1
* @param i2
*/
const swap = (i1, i2) => {
const v = arr[i1];
arr[i1] = arr[i2];
arr[i2] = v;
};
/**
* To heapify a subtree rooted with node
* @param {number} n size of heap
* @param {number} i an index in arr[]
*/
const heapify = (n, i) => {
const l = 2 * i + 1; // left = 2*i + 1
const r = l + 1; // right = 2*i + 2
let largest = i; // Initialize largest as root
// If left child is larger than root
if (l < n && arr[l] > arr[largest]) largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest]) largest = r;
// If largest is not root
if (largest !== i) {
swap(i, largest);
// Recursively heapify the affected sub-tree
heapify(n, largest);
}
};
// Build heap (rearrange array)
for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--) heapify(arr.length, i);
// One by one extract an element from heap
for (let i = arr.length - 1; i > 0; i--) {
// Move current root to end
swap(0, i);
// call max heapify on the reduced heap
heapify(i, 0);
}
return arr;
};
return heapSort(_arr);
})(Array(100).fill(null).map(() => Math.round(Math.random() * 100)));

